学习理论

1 偏差/方差权衡

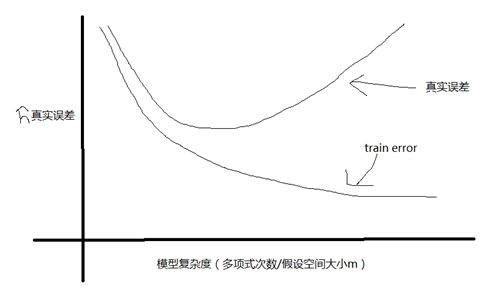
对于我们前面介绍的欠拟合和过拟合的问题，代表着两种误差较大的建模方法。对于欠拟合来说，在模型结果和样本内结果误差较大，可以推论为在模型结果和实际结果误差较大，这种成为偏差（bias）。对于过拟合来说，虽然模型结果和样本内结果误差较小，但是由于样本的不确定性和随机性，样本的结果不能反映真实世界的结果，所以存在方差（variance）。真实误差（generalization error）主要有偏差和方差构成，一般来说，需要在偏差和方差之间进行权衡，如果模型太简单（或参数太少，欠拟合），容易出现比较大的误差和比较小的方差；如果太复杂，容易出现较小的误差和较大的偏差。

学习理论主要是通过一些直觉的经验或者推导出来的规则，使我们可以根据不同的情景最好的应用学习算法。主要是为了回答以下问题：

1 我们是否可以正式的权衡偏差和方差，也就是说自动选择一个合适的模型。

2 在学习算法中，真实误差是最重要的，但是大部分学习算法都根据训练样本进行学习。训练样本和真实误差之间的关系如何。

3 在哪些情况下学习算法可以较好的工作。

首先我们介绍两个定理：

联合界限定理：A1，A2….Ak分别代表k个不同的事件，则：P（A1UA2U….UAk）<=P(A1)+…..+P(Ak)

Heoffding不等式（中心极大值定律）：Z1,….Zm为m个独立同分布的随机变量，并且服从伯努利分布。即P(Zi=1)=φ,P(Zi=0)=1-φ。令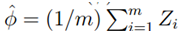表示这些随机变量的平均值，同时给定常量r，则：

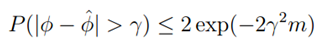
为了方便表述，我们这里讨论的都是二值分类，也就是说y={0,1}。

对于一个训练集来说，我们定义训练误差（training error）为训练集中次数出现的概率/频率：

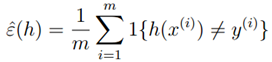
同时，我们定义真实误差(generalization error)，物理意义可以理解为当出现一个新的样本并且符合D分布时，h可能分类错误的概率：

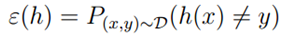
现在考虑先行分类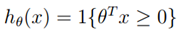，，一个获得合适的参数?的方法是使训练错误最小，我们称之为经验经验风险最小（ERM）过程。

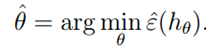
同时，在下面的学习理论的介绍中，我们不考虑具体的假设参数，也不考虑我们是否使用的是线性分类模型等。我们定义假设空间H，学习算法将在假设空间中找到一个合适的假设函数（包括了参数和模型）。

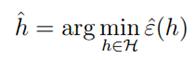
2 有限假设空间

首先我们考虑有限假设空间的学习问题，有限假设空间包含k个假设函数H=｛h1,h2,…hk｝。函数从特征空间X映射到｛0,1｝，而ERM试图寻找一个使训练错误最小的假设函数。下面我们根据训练集对于真实误差给出一些保证，1)我们发现训练误差和真实误差相近；2)对于假设函数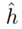，真实误差存在上界。

对于任一假设空间中的函数hi，令。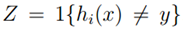

则训练错误可以表示为：

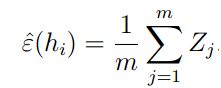
因此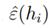，可以理解为m个从独立同分布的伯努利分布的随机变量Zj的平均，而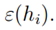是这个伯努利分布的真实平均值。则由中心极大值定律可知：

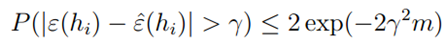
由上式可知，对于某一假设函数hi，如果样本量m较大，训练误差有很大的概率约等于真实误差。现在将某一个假设函数推广为所有的假设函数。我们用Ai表示事件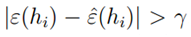，则使用联合界限定理，有：

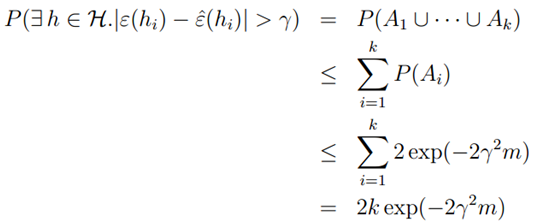
可以进一步推导出：

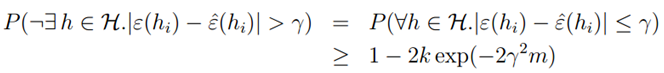
也就是说，（一致收敛uniform convergence）对于假设空间的所有假设函数h，训练错误约等于真实错误的概率（置信度）大于某个值。

在以上的讨论中，我们是给定一个样本量m和r，获得了一个误差的可能性，即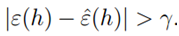的最大概率界限。同时，我们可以通过两个参数，获得任一个参数的界限。比如给定r和置信度σ，我们需要多少样本量m才能保证在概率1-σ下训练误差和真实误差之差小于r。我们获得了以下公式：

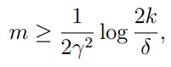
（样本复杂度）上式说明了样本数量m大于某个界限时，可以有1-σ的概率保证，对于所有假设空间里的假设函数，训练误差与真实误差之差小于r。同时上式也说明了需要的样本数量只与假设空间中的假设函数数量成log关系，即使k很大，m增长的也比较慢。

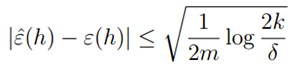
下面，我们定义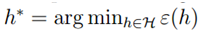即h*具有最小的真实误差，也就是物理意义上最好的假设函数。假设一致收敛成立，则：

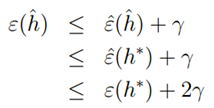
上式1、3步试用了一致收敛，第二步根据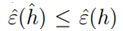。我们可以获得以下结论：如果一致收敛成立，则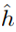的真实误差最多比最好的假设函数h*差2r。将上式扩展，可得到以下定理：

定理 对于|H|=k，给定m和σ，则在置信度1-σ有：

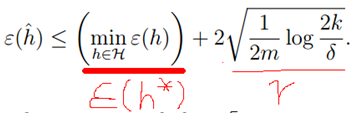
同时，以上模型可以和我们以前介绍的偏差/方差相对应。当假设空间即k增大时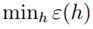，只能减小，因为可能找到一个使误差更小的函数（和偏差对应），但是第二项会增加（方差）。

注：第一项的真实物理意义其实是最好的函数的真实误差，也就是其实我们想知道的。但是我们没法获得最好的函数h，我们只能使用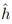来评估。其实我们最后获得的是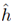而不是h.

3 无限假设空间

在以上的论述中，我们仅考虑了有限的假设空间，而在现实应用中，大部分都是无限假设空间。比如线性分类，每个参数都是一个实数，则得到了一个无限假设函数空间。

在有限的假设空间中，我们使用的是假设空间中假设函数的个数来表示的假设空间复杂度（模型复杂度）。而在无限假设空间中，我们使用一个新的值度量假设空间的复杂度——VC维。

VC维的定义为：在实力空间X上的假设空间H，VC(H)表示可被H打散的X最大有限子集大小。如果X的任意有限大的子集可以被H打散，则VC（H）为无穷大。

如果我们要证明VC(H)大于d，我们仅仅需要证明存在至少一个大小为d的集合可以被H打散。

比如在二维空间上的线性分类函数集合，在二维空间上存在三个点的集合可以被一条直线随意划分（除非这三个点在一条直线上），而对于任意一个四个点的集合，直线都无法对其进行随意划分。所以线性分类函数的VC维为3。

在以上基础上，我们可以获得以下结论：（证明略）

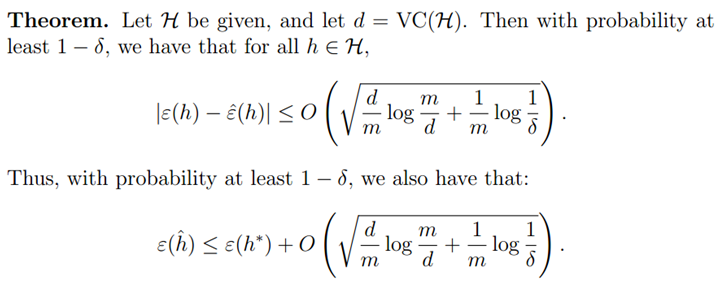
由上面可知，如果假设空间存在有限的VC维，则一致收敛随着m的增加而出现。同时，可以获得关于样本复杂度的以下推论：

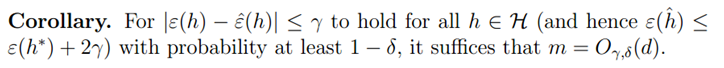
也就是说，为了获得较好的学习结果，样本数量和VC维成线性关系。同时，对于大部分合理的假设空间，VC维与模型的参数成线性关系。

附：以上所有的结论都是在ERM模型基础上得出的。视频中同时介绍了逻辑回归和SVM算法。SVM算法虽然具有无限的特征空间（kernel函数），但是由于它只考虑间隔较大的分类函数，所以VC维也比较低。