规则化和模型选择

目前我们已经学习了很多机器学习算法，比如线性模型、神经网络、多项式回归模型等。当我们要解决一个机器学习问题时，首先需要选择一个适合恰当的模型，有些模型还需要选择参数，比如局部加权回归中的bandwidth等。

问题：在有限的模型集合M=｛M1,M2,…Md｝中为问题选择一个最合适的模型Mi。

1 交叉验证

对于以上问题，如果选择使用经验风险最小化（ERM）方法， 在所有的模型中选择具有最小训练误差的模型，似乎是可以的，但是是不可以的。因为选择最小的训练误差往往具有较高的方差，即选择较高次数的多项式模型，出现过拟合现象往往具有较大的真实误差。

可以使用简单交叉验证方法（hold-out cross validation ,also called simple cross validation）：

• 随机分割样本集S为训练集(70%)和测试集(30%)。
• 使用训练集训练各个模型，分别获得假设函数。
• 对假设函数通过测试集进行验证，选择最小误差的模型。

通过使用测试集对假设函数进行验证，我们更好的评价了假设函数的真实误差。同时，也可以选择最小误差的模型以后再使用所有的样本对模型进行学习。简单交叉验证的缺点是数据集的浪费，即使我们在选择模型完成以后在使用所有的数据进行再学习，但我们在选择样本时使用的训练集只是所有的数据集的70%。

为了节省数据，以下是k-fold交叉验证：

• 将样本集分割成k份，每份有m/k个样本。样本子集为｛S1…..Sk｝
• 对于每个模型Mi，对其使用如下评价：
  • 对于每个样本子集Sj：使用除Sj的其他所有样本子集S1US2U…Sj-1USj+1U…USk对模型进行训练并获得假设函数hij。
  • 使用hij（over j）真实误差的的平均值评价模型Mi的真实误差。
• 选择具有最小真实误差的模型Mi，并通过所有的数据集S对模型进行训练获得最终的假设函数。

对于上述算法，常用k=10。但是在极端情况下，比如样本数据极少极为昂贵，可以将m个数据样本分为m份，每份只有一个样本，每次使用m-1个样本进行训练，使用1个样本进行测试。我们称之为leave-one-out交叉验证。

2 特征选择

特征选择是模型选择的一个特殊但重要的例子。比如当我们有一个监督学习问题，特征空间维度n很大，而且怀疑只有一些特征和学习任务，但是同时数据样本量还小有关。即使我们选择最简单的线性，假设空间的VC维也是O（n）。除非训练集很大，要不就可能出现过拟合的问题。

因此，我们需要通过特征选择算法减少特征的数量。假设当前有n个特征，如果使用遍历所有可能的特征组合并使用交叉验证选择特征的话，有2^n可能的组合，这样做不靠谱。比较靠谱的是使用启发式算法。

向前搜索算法：

除了向前搜索算法，还有向后搜索算法，即初始化F为全部特征，然后重复的删除一个影响最小的特征。这两种算法被称为wrapper model feature selection，因为它们是一个报过了学习算法的算法。这种算法一般可以获得比较好的结果，但是时间复杂度很高，因为它需要O(n^2)次调用学习算法。

过滤特征选择算法通过是计算每个特征的S(i)来评价特征i对区分y的重要性。只需要计算所有特征的S(i)并选择重要性（S(i)）最高的一些特征。

我们可以定义S(i)为Xi和y之间的关联度，并通过训练集进行计算。比如，我们可以计算xi和y之间的相互信息作为S(i)：

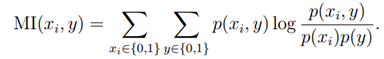
在以上公式中，我们假设xi和y都是二值的，比如垃圾分类情况，相关的计算都可以根据训练集预测。

同时，相互信息也可以用KL距离(kullback-beibler divergence)，也就是两概率分布之间的差异表示：

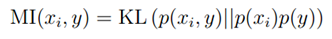
通过计算p(xi,y)和p(xi)p(y)之间的差异，可以获知xi和y之间的依赖程度。如果p(xi,y)等于或约等于p(xi)p(y)，则说明它们是独立的，表示无依赖，则S(i)很低。

3 贝叶斯统计和规格化

这一节中，我们介绍一个防止过拟合的新方法。此方法的本质就是在假设?是随机变量而给他一个先验概率如高斯分布N(0，xx)，这样参数就会接近于0从而防止出现了过拟合现象。

在前面，我们使用最大似然估计找到样本出现概率最大的参数：

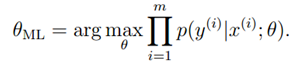
这里是将参数?看成未知的常量，也就是我们想要求出的（频率学派）。

另一种方法去估计参数的方法是从贝叶斯学派的角度，认为参数?是位置的随机变量。使用p(?)表示参数?的先验概率，比如猜测?服从高斯分布；然后根据样本集获得参数的后验概率：

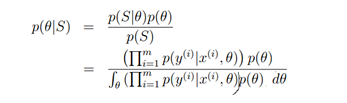
当对于一个新的样本X并希望预测y时，可以基于训练集S计算不同y的概率(计算出现?的概率并乘以在?情况下基于x出现y的概率，然后积分?，即求基于所有?求y概率的期望值)：

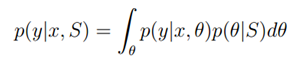
然后计算y的期望值（对于离散值使用累加代替积分）：

????

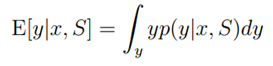
上面的过程我们可以看作完全贝叶斯预测过程，将参数?看作随机变量，对所有的?后验概率，然后根据?求y的期望值。但在以上过程中，所有的计算都非常困难。因此，在实际使用中，我们常常估计?的概率并找到基于训练集S参数?最可能的情况，也就是找到使后验概率p(?|S)最大的参数?：

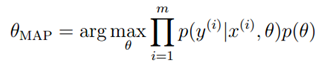
计算出了参数?，在根据x预测y时就可以直接使用假设函数。

上式和最大似然性估计的公式几乎相同，只不过在最后加入了?的前验概率p(?)。在实际使用中，我们常常假设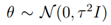，这样的话，参数会大部分接近0，这和参数选择的思想是一样的，也就防止了出现过拟合的现象。

比如在文本/邮件分类的学习问题中，有5000个feature，可能里面的大部分feature都是没用的，所以我们给他先验概率（假设）认为他们大部分接近于0，这样就和特征选择获得了差不多的效果。（特征选择对于不重要的特征的权值置为0，而这个方法对于不重要的特征权值接近0）