密度估计-混合高斯分布和EM算法

密度估计就是计算样本空间某区域内的密度，即可以估计出一个新的点落入这个区域的概率，或者说对于一个点这个点出现的概率（如不正常发动机检测）。混合高斯模型就是描述这种密度估计的概率模型，此节中我们讨论EM（最大似然算法）算法 在密度估计方面的应用。

对于无监督学习的一个训练集｛x(1),x(2),…x(m)｝,混合高斯模型是通过引入一个隐含(latent)的随机变量z(i)来描述x(i)可能属于某一个高斯分布。与监督学习算法GDA模型中的硬指定不同，z(i)在这里也是随机变量，我们假设他服从多项式分布。

P(x(i),z(i))= P(x(i)|z(i)) P(z(i))，其中，x(i)|z(i)=j服从高斯分布N(uj,∑j)，z(i)属于多项式分布Multinomial(φ)。

对于给定参数u,∑和φ，我们数据的似然估计是：

加入我们已经知道了z(i)是什么（其实是一个随机变量），以下参数可以使似然度最大化：

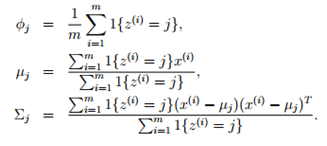
其实，如果z(i)给定的话，最大似然估计和我们估计GDA模型的参数的方法几乎相同，不同点如下：我们使用z(i)表示点的label，而不是y(i)；对于不同的高斯分布，混合高斯模型中的不同高斯分布的协矩阵不同。

然而，我们以上的结论是基于z(i)给定，而在我们的问题中z(i)是未知的。

可以使用EM算法。EM算法是一个包含两个步骤的迭代算法，在步骤E中，首先尝试猜测z(i)的值。然后在步骤M中，根据猜测到的z(i)更新模型参数，使似然最大。

在步骤E中，可以使用贝叶斯规则计算Z(i)的概率：

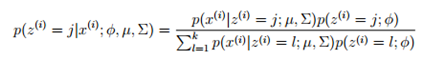
在步骤E中，我们并没有计算出z(i)的值，而是计算z(i)的概率，在步骤M中，使用概率来表示个数，这个应该还是比较好理解的。

与k-means聚类算法相比，EM的结果不是一个"硬的"聚类结果，而是属于某一类的概率。

K-means和EM算法的关系

问题：将样本X分为k个类。K-means是通过为x硬指派一个类别c，而EM算法计算x属于某一个类别z的概率。

直白地说，聚类问题就是为样本分配隐含类别c/z。两个算法都是通过迭代的方法，每一次迭代分为两步。

对于EM算法，我们首先假设样本X的隐含类别为z，并通过度量样本的极大似然估计来评价，也就是联合分布p(x,z)。但随机指定的z不一定使p最大，因此我们调整参数使p最大。调整参数以后，我们可能会发现更好的y的指定，然后我们重新指定y，然后在计算使p最大的参数。如此迭代。

对于k-means算法，我们首先将随意选择聚类中心点，然后根据样本离那个中心点最近将样本分配给该类别（概率最大），即样本属于该类别的可能性最大。然后重新计算聚类中心点，然后再分配样本。

由上可知，EM算法和k-means算法思想上有一定的相似性。