增强学习

和监督学习相比，监督学习可以针对一个样本定义正确或错误，但是在增强学习的问题中，无法告知agent当前的动作是正确还是错误的。如下棋，对于某一步来说，无法评价这一步是对还是错，只能根据结果，对每一步给定一个评分，告知agent这一步是比较好，还是比较差。

增强学习要解决的问题是：一个能够感知环境的自治agent，如何通过学习选择能达到目标的最优动作。增强学习的目标是获得一个控制策略，以选择能达到目的的行为。

1 马尔科夫决策过程（MDP）

马尔科夫决策过程由五元组｛S,A,｛P_sa｝,r,R｝构成

S表示状态集（states）。

A表示动作集（actions）。

P_sa表示状态转移概率。状态s根据动作a转移到其他状态的概率分布。（动作a为s1->s2，并不是说一定转移到s2，还有一定的概率转移到其他状态）

r~[0,1)，阻尼系数，代表着离现在越远的状态对现在的影响越小。

R：SxA->R，R是回报函数，回报函数表示状态s进行动作a的评分。因为一个策略对于一个状态的动作是确定的，所以回报函数只与状态有关，可以写为R：S->R

马尔科夫决策过程如下，对于初始状态s0，根据策略选择一个动作a0，执行动作后根据P_sa转移到状态s1，一次循环….

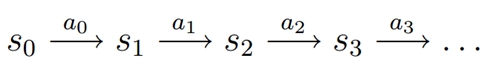
对于状态序列，所有状态的回报之和为：

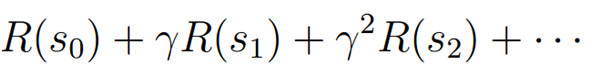
增强学习的目的就是选择一个动作序列（策略），使回报累积期望值最大：

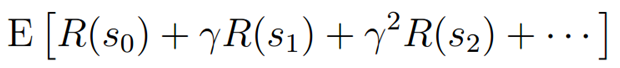
对于一个给定的策略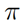（Pi）的评价函数来评价这个策略的好坏，定义为

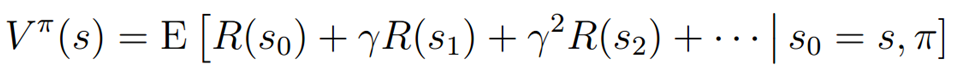
该式满足Bellman等式：

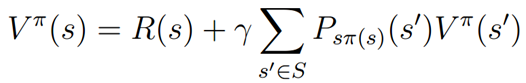
该式说明策略的评价函数包括当前状态的汇报和使用该策略以后的回报期望。

同时，我们定义最优评价函数为：

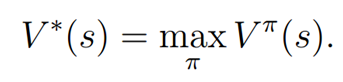
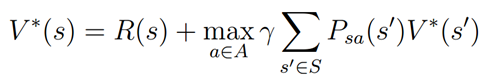
对应最有评价函数，我们定义状态s的最优策略

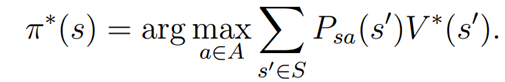
对于不同的初始状态s0，他们的最优策略是一样的。

2值迭代算法和策略迭代算法

下面将介绍两个解决有限状态MDP的高效算法，只考虑具有有限状态和动作的MDP。

值迭代算法

内部循环有两种更新方法：

• 首先计算所有状态的评价值，等此次迭代的所有状态的值计算完成后，一起更新。
• 计算某一个状态的评价值，然后立马更新该状态的评价值。

通过一系列的迭代，最终V将收敛于V，而基于V我们就可以计算出最优策略。

策略迭代：

策略迭代和值迭代相似，只不过策略迭代聚焦于策略，设法使策略Pi收敛到Pi*。

在第二步循环里面，首先基于当前策略计算每个状态的评价值，然后根据所有状态的评价值计算更新策略。其中2(a)步骤可根据bellman等式计算，对于每个状态写一个线性方程，如存在n个状态，则存在n个n元线性方程组成的方程组，可通过解这个方程组计算得到结果。

比较：

两种方法相比，策略迭代更适合较小规模的MDP，而值迭代更适合大规模（状态很多）的MDP，因为值迭代不用求线性方程组。

3 参数估计

在现实数据中，通常状态转移概率和回报函数通常是非已知的，而状态集、动作集和阻尼系数是已经设定好的。因此，我们需要通过已知样本去学习计算状态转移概率和回报函数。

样本格式：

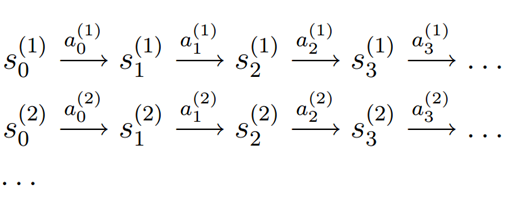
状态转移概率的计算方法为：

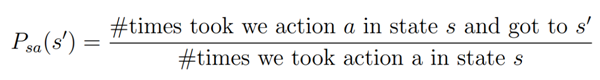
如果回报函数非已知，可使用同样的方法求状态s的观测到的回报的平均值作为该状态的回报。

将参数估计和值迭代结合起来，可以得到以下算法：