Generative learning algorithms

对于前面的算法，都是学习p(y|x)或者接学习一个从输入X到输出类别的算法，这种算法叫discriminative learning algorithms。

而存在另一种算法，这种算法首先为不同的分类建立不同的模型，对于一个新的需要判别的对象，计算它和哪一个模型更相似即可。

公式表达如下：

假设y=｛0，1｝

我们首先根据训练集为p(x|y)和p(y)建模，然后根据贝叶斯法则：p(y|x)=p(x|y)p(y)/p(x)

P(x)=p(x|y=1)p(y=1)+p(x|y=0)p(y=0);

其实，在对输入x进行分类时，我们只希望使p(y|x)最大的y。可以不考虑p(x).

即：

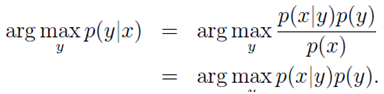
1 高斯判别分析GDA

在此模型中，我们假设p(x|y)属于multivariate normal distribution。

即：

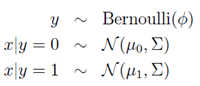
因此，有：

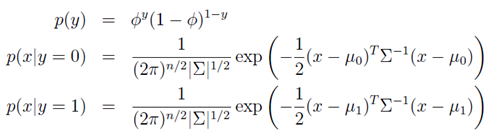
为了求出相应参数，我们使下式最大化。

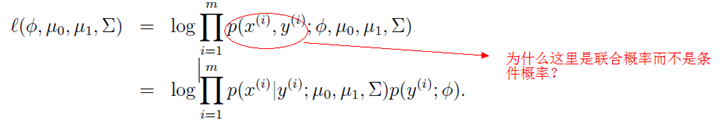
下图是一个GDA模型的例子，因为两个高斯分布使用同一个∑，所以他们的shape是一样的。但是他们的u0和u1不一样。

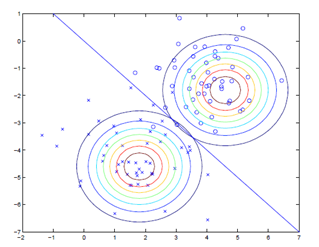
和逻辑回归相比，GDA需要更严格的假设，如果假设成立，也可以获得更好的结果。

2 朴素贝叶斯

在GDA中，特征向量x是连续的实数。而在朴素贝叶斯中，特征向量是离散值。

下面以垃圾邮件分类为例举例说明。

设置描述邮件的特征向量x为50000个单词字典，如果邮件中存在某个单词即设置为1：

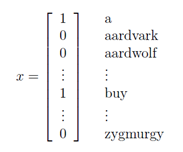
同时，假设每个特征与其他特征是相互独立的（贝叶斯假设）。如果不独立，则需要(2^50000-1)个参数。

则

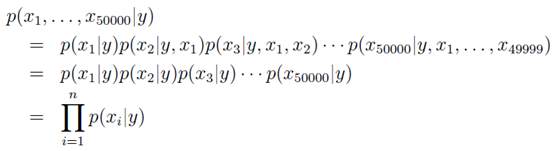
同时我们使用,和。这里的下标i不代表着第i个样本，而代表着第i个特征(word)。和下面的变量j对应。

只要使下式最大化：

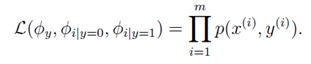
则可得到参数（从物理意义也可以解释）。

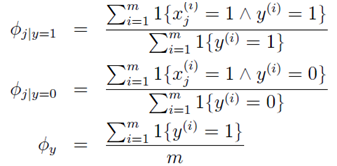
计算出三个参数向量以后，如果需要预测一个新的对象x，只需要带入下列公式计算p(y=1|x)和p(y=0|x)，并比较即可。

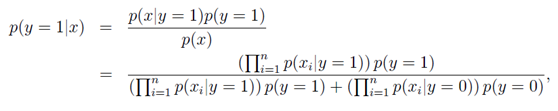
最后说明一点，虽然例子中特征向量X中的对象Xi只能为0或1，但是Xi也可以是多个不同的离散值。即使特征元素是连续值，也可以将连续值根据阈值分为离散值然后使用贝叶斯分类器。

2．1 Laplace平滑

由于训练集数量的问题，有些特征出现的概率可能较小而在这些训练集中没有出现，这时不应该认为在训练集中没出现过的事件的概率就为0。

在计算特征出现的概率时，分子加1，分母加k。k为特征可选取的集合元素个数。

物理上可以这么考虑，如果训练集个数足够小，比如没有训练集，则特征出现的概率为1/k。

如：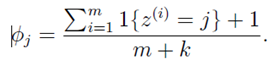

2.2 Event models for text classification

在文本分类问题中，文本特征的建模可以使用不同的模型从而达到更好的效果。

如在前面的叙述中，我们使用的模型是multi-variate Bernoulli event model。此模型可以将邮件的生成方法看为：1）首先随即决定邮件是否为垃圾邮件。2）然后遍历字典中的每个单词，根据概率决定每个单词是否包含在这个邮件中。因此，一个邮件的概率为：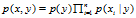

下面提出一个更好的模型，叫multinomial event model。此模型Xi表示邮件中第i个单词在字典中的ID。此模型中的邮件生成方法可以看为：1）随机决定邮件是否为垃圾邮件。2）邮件发送者随即写下第一个单词。3）重复第二步。邮件的概率为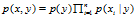：。虽然此模型的邮件概率同上一个模型一样，但是变量所代表的含义不相同。

参数如下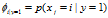：for any j, 和。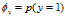

则最大化：

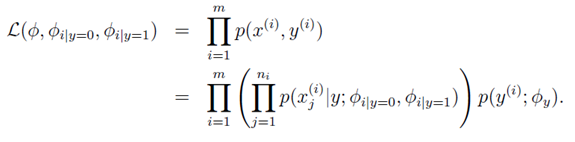
得出：

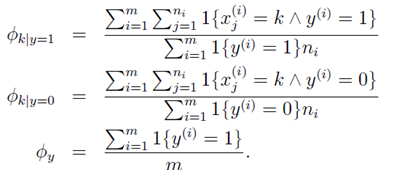
从公式上来看，参数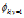的物理意义：分子是所有垃圾邮件的样本中单词Xj=k出现的次数。分母是所有垃圾邮件的单词数。

如果使用Laplace平滑，可得到以下结果：

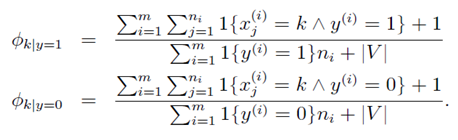
第二个模型比第一个模型好的原因可能是：第二个考虑了邮件中单词出现的次数。

3 神经网络

视频中简单介绍了神经网络的概念，我将视频上讲的大体记录一下，讲义中没有相关介绍。

目前我们介绍的都是线性划分，而神经网络是一种非线性划分。

线性划分如下：

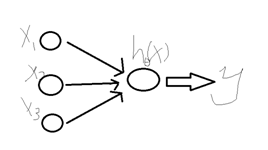
而对于神经网络：

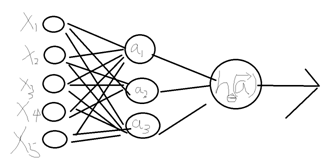
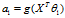
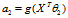
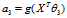
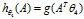
求出四个参数使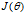最小。

这就是一个非线性的划分。