主成分分析
主成份分析(principal component analysis,PCA)算法和因子分析算法有些相似,都是在低维空间上表示高维空间的数据。但是主成份分析算法更加直接,直接去寻找高维特征之间的依赖关系,从而达到降维的目的。
比如在一个对飞行员的调查中,skill和enjoyment之间有一定的依赖关系,因此我们可以试用u1(飞行员资质)这一个特征来表示前面的那两个特征,u2可能代表着一定的误差。

1算法
1.1数据的预处理
在使用主成分分析对数据降维前,由于各特征值的物理意义不同,因此要对其进行预处理。

1.2 找到数据位置的方向
数据处理以后,下一步就是找到数据位置的大概方向,或者说单位向量u。我们希望样本数据在这个方向上的投影的方差(variance)最大化,或者说样本数据离这个方向的直线距离最短。物理意义:方差较大可以获得更多的信息?
样本x在方向u上的投影到圆点的距离为xTu,为了最大化投影的方差,我们希望找到单位矩阵u使下式最大化。
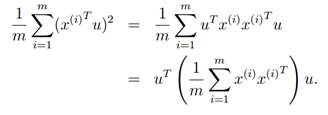
令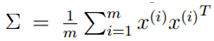 ,而u为单位向量,则上式的最大值代表着∑的非特征值,u代表着主特征向量(特征值最大的特征向量)。
,而u为单位向量,则上式的最大值代表着∑的非特征值,u代表着主特征向量(特征值最大的特征向量)。
从上面分析,为了获得1维的子特征空间,就去找最大特征值的特征向量。那如果找k-维的子空间,只需要去找top-k特征值的特征向量u1,u2,…uk。
注:因为∑是对称的,所以这些特征向量是正交的。
找到了k个特征向量,我们就可以在k维空间上表示原高维空间的样本x(i):
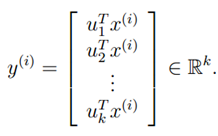
由上可见,PCA算法是一个降维算法,我们找到的k个特征向量u1,u2…uk成为主成分。
1.3 算法
总结以上内容可见,PCA算法分为三步:
1 预处理
2 计算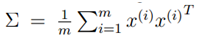
3 找到∑的k-top特征向量
2 CPA的应用
CPA可用于多种目的,比如
- 数据压缩:降维
- 可视化:把特征压缩到2或3维空间爱你
- 机器学习中通过降维防止过拟合。
- 匹配/距离计算:在子空间计算两点的距离。
2.1 Latent semantic indexing(LSI)
将CPA算法应用在文本处理中,如对于一个文本,首先创建其向量字典:

这里一般省略预处理阶段。
若我们希望比较两文本x(i)和x(j)的相似性,比如我们使用两文本的字典向量的内积表示。
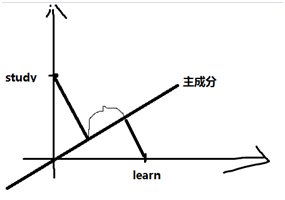
对于两个只含有一个单词的文本:"study"和"learn",字典也仅含这两个单词(2维空间),那如果仅仅计算内积,则相似度为0。
但如果将2维空间变为1维,映射到主成分上,则发现他们之间仍具有一定的相似性。
3 CPA的实施
在使用CPA算法时,若原特征空间为10000,则∑为10000*10000维,计算量非常大。
因此,可以使用奇异值分解的方法简便的计算。
对于训练集{x(1,x(2),…x(m))},令:
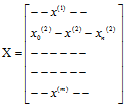
则∑=XTX
因此,V的top-k列就是∑=XTX的top-k特征向量。X=UDV。
SVD性质:

4 算法的比较
| 密度估计算法 | 非概率算法 | |
| 数据可用子空间表示 | 因子分析(异常分析) | 主成分分析(降低维度) |
| 数据可分为块或团 | 混合高斯模型 | K-means |