一 概述及问题提出
支持向量机的原理是找到一个划分（我们假设训练集是可分的），使离这个划分几何最近的训练集元素点（称为支持向量）与划分的距离最远。本文首先介绍了支持向量机的数学计算目标，然后介绍如何通过拉格朗日对偶、kernel函数以及SMO算法有效的得出支持向量机的计算结果。其中拉格朗日对偶和SMO算法是求解支持向量机的方法，kernel是优化（或者说是快速）计算结果的一种方法。
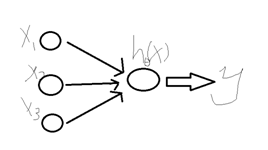
在解决支持向量机的问题上，我们使用了一种新的符号。首先分类结果y=｛-1，1｝，其次，线性分类的参数不使用?而是用?和b，分别代表了?(1-n)和?0。分类器如下：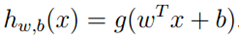
，如果z>=0,g(z)=1,否则g(z)=-1。这个分类器模型是直接预测分类结果，而不像前两章那样预测每个分类的概率。
我们的目标就是获得参数w和b。或者说，机器学习算法的目标就是根据模型和训练集获得模型的参数！
现在我们定义函数margin和几何margin，直观的说，支持向量机就是使训练集的margin最大。函数/几何margin虽然从数值上可能不一样，但是它们之间成比例，所以，求最大化不需要区分函数或几何margin。
函数margin：对于一个训练集元素：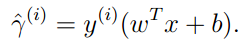
对于一个训练集的margin
。
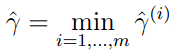几何margin：几何margin就是在几何上计算点与划分直线的距离。
，
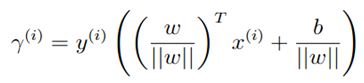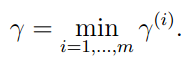
为了获得更好的分类，有上面所说，我们希望获得一个最大的margin。
可以使用一下公式：
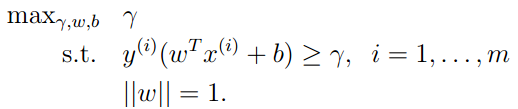
我们不要求||w||=1，这样不可以使用现有的求最优解方法。我们使用以下公式：
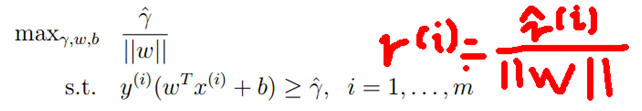
因为我们是求margin的最大值，由margin的定义可以知道，我们可以给参数w和b分配任意的倍数，因此我们假设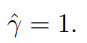
。（因为通过调整w和b总能获得这个结果）。这样，我们就获得了以下公式：
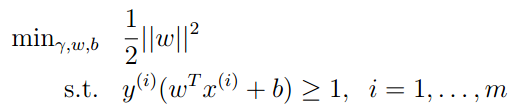（1）
通过一系列的转换，我们可以通过求最优化问题(1)求出参数w和b。这样，我们就获得了最优的分类器。
下面将要介绍如何解决最优化问题（1）。
二 拉格朗日对偶
为了解决上一节中提出的基于约束的最小化问题，我们可以使用拉格朗日对偶定理，使参数原先的多参数优化问题编程单参数优化问题，并通过内积快速计算结果。首先计算对偶问题，计算出拉格朗日乘数，然后求出原参数w和b。最本文的最后结果中，我们会得到问题（1）的对偶问题，在对偶问题中，我们发现计算内积<X(i),X(j)>是关键环节。我们在下一节会介绍使用kernel函数计算内积的方法。
对偶问题的说明和相关证明我会在最后一节进行介绍。
首先将最优化问题（1）的约束我们定义为：
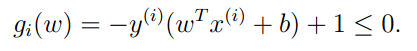
构建拉格朗日函数：
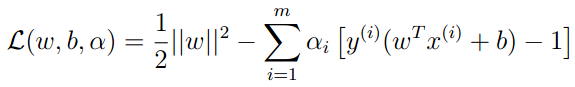（2）
对于原问题，我们首先要求出对于a函数L的最大值。直观的说，要求最大值（2）式中的后项（背减的项）如果是0，（2）式将最大。因此，当gi（w）！=0时，我们使ai=0.当ai！=0时，则gi（w）=0，即此点为支持向量。
要求出此问题的对偶问题，首先固定a并根据w和b最小化函数（2）。可以通过对函数L偏导为0，则：
=》
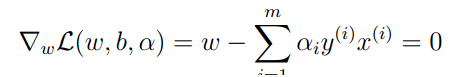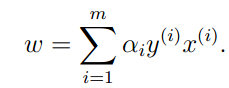（4）
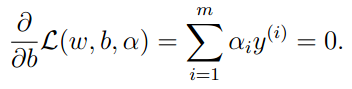
将上列结果带入原拉格朗日函数，获得：
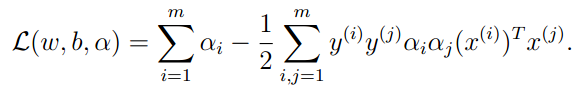
这样，我们可以获得问题(1)的对偶问题：
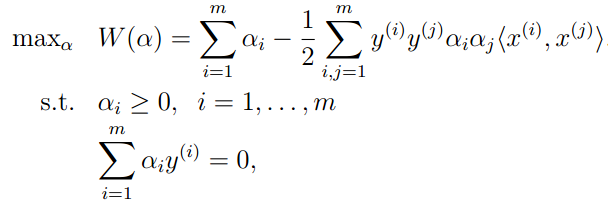（3）
可以证明，在本文的最优化问题中是符合对偶问题等于原问题的条件的（KKT），因此，我们可以通过解决对偶问题解决原问题。当我们可以解决最优化问题（3）的时候，我们获得了参数a，就可以根据公式（4）计算出w并进一步计算出b的值。
现在让我们看看对于一个新的input，如何进行预测。首先我们要计算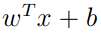
并根据他的值预测最终分类。根据公式（4）可知：
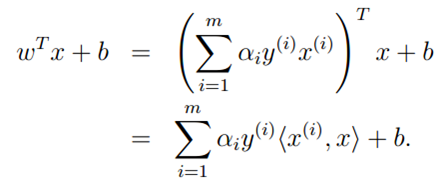
因此，如果我们计算出了a的值，就可以进行预测。同时，对于a大部分分量都是0，只有对于支持向量a才不是零，只需要计算少量的内积就可以获得最终结果。
三 Kernel
在上节中，我们发现要SVM算法的计算需要计算各训练集元素之间的特征向量的内积，而kernel函数不仅可以快速计算原始特征向量的内积，而且可以计算高维高阶特征向量的内积，并同时保证时间复杂度为O(n)。
使用kernel函数很简单，只要选择一个适当的kernel函数，并且将最优化问题中的所有内积改为kernel函数，然后继续计算SVM算法就可以了。
使用kernel的好处就是：可以将原始特征向量转化为高阶的特征向量，并且可以解决非线性分类的问题。因为在原始特征向量空间中，分类问题可能是非线性的，而到了高维（高阶）空间中，分类问题可能使用线性分类解决。
Kernel函数的表示形式是：
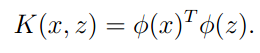
其中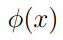
代表着原始特征到高阶特征的映射，我们称之为特征映射。（很明显，使用高阶特征可以获得更好的精度并解决非线性分类问题）
下面我们举几个kernel函数的例子来说明使用kernel函数计算内积的方法。
例1 我们设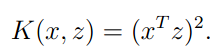
，其中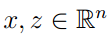
则：
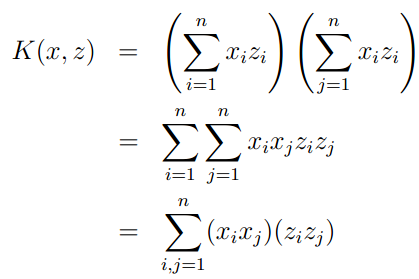
我们可以将kernel函数写成标准函数，其中特征映射函数为
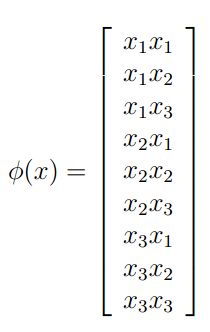
由此例可以看出，如果我们直接计算高维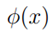
，则需要O(n^2)，而计算kernel函数则只需要线性时间O(n)。
例2
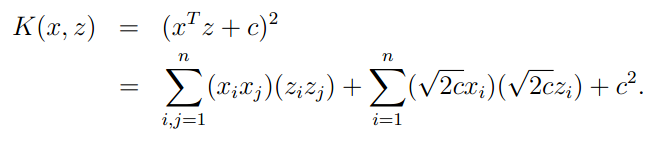
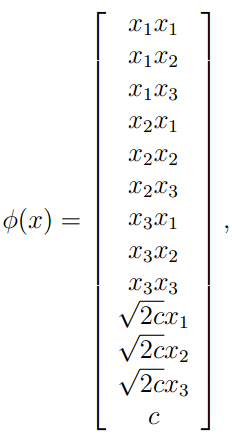
直观的说，kernel函数求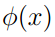
和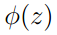
内积，也可以理解为求他们的相似度。因此，我们可以使用下列公式。（我们成为高斯kernel）
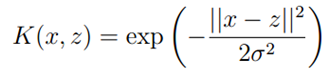
四 训练集不可分解决方法
在以上所有论述中，我们都假设训练集时可分的，而在真实的环境中，往往无法得到这个要求（不可分）。还有一种情况，虽然训练集是可分的，但是由于一个特例的影响，我们获得的划分结果明显不是我们希望的，如下图，左图是一个较好的划分，而右图因为一个特例的引入导致划分变化很大，其实我们希望可以忽略或者减小这个特例的影响。
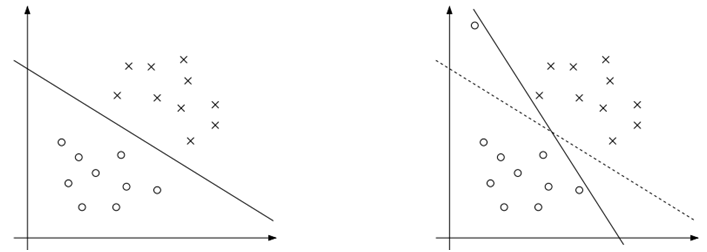
为了解决数据不可分和减小异常值的影响，我们对原优化问题进行了调整提出了新的优化问题。（5）中我们允许margin小于1，但是会对目标函数增加一个惩罚值。
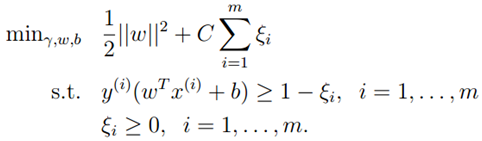（5）
我们可以得到拉格朗日函数：
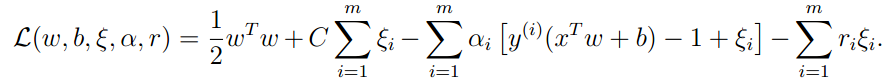
我们获得上式的对偶问题如下：
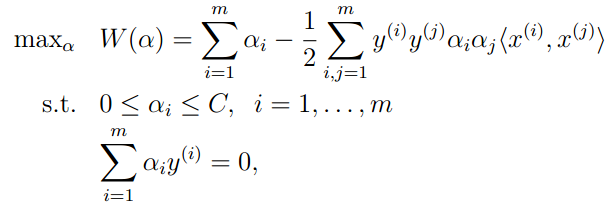（6）
五 SMO算法（sequential minimal optimization）
1 坐标上升法
坐标上升法和我们以前介绍的梯度算法和牛顿算法一样，都是最优算法。坐标上生法的目标函数为：
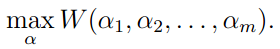
它的原理是根据一定的规则选取ai，并固定除了ai其他的所有参数，找到使W函数最大的ai，循环任务直至收敛。
2 SMO算法
综上所述，SVM算法是想解决最优化问题(6)，我们可以根据坐标上升法求解。因为在此问题中，某一个参数可以通过其他n-1个参数计算得出，所以我们在此问题中需要同时改变两个参数
SMO算法如下：
我们现在假设我们选取根据a1和a2计算W的最大值，并将a3…am固定。因此，根据(6)中的约束可知：
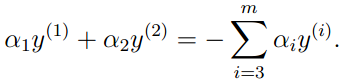
由于右项都是常量，可以用下式表示：
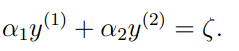
如果y(1)和y(2)异号，则a1和a2的限制如下图所示
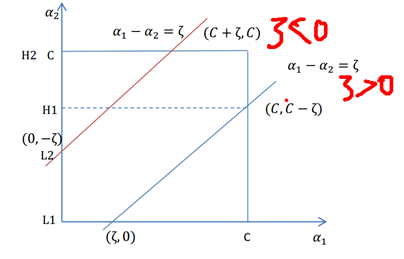
令L<a2<H，则：
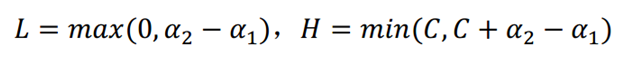
同理，若y(1)和y(2)同号，则
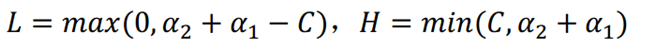
用a2表示a1，则：
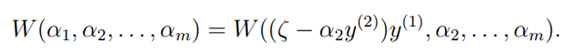（7）
在公式(7)中，a3…am是常数，而由公式（6）可以看出，公式（7）是关于a2的一元二次方程，而要求是W最大化的a2可以直接使用公式获得。最后，根据a2的约束，就可以获得最终a2的值，然后就可以求出a1的值。
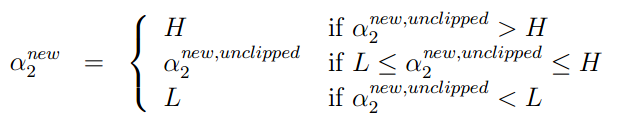
六 拉格朗日对偶的证明和解释
首先介绍对于等式约束的极值求解方法。对于有条件的最小问题：
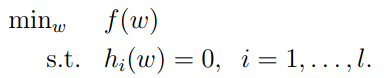
可以使用拉格朗日乘数方法解决。令拉格朗日函数为：
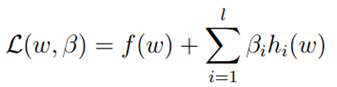
令函数L的偏微分为0，就获得了最终的结果：
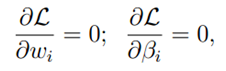
下面将上面的结果推广到不等式条件的情况下。假设原问题为：
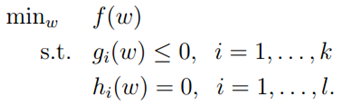
定义拉格朗日函数为：
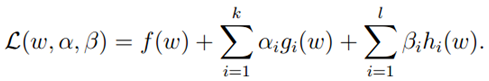
令
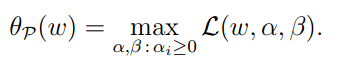
则如果w违反了任何约束，则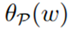
为无穷大。
如果w满足所有约束，则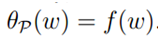
综上所述：
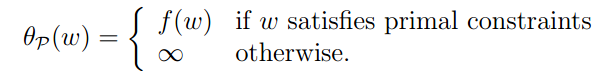
因此，如果我们最小化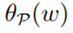
，则变成了和原问题同样的问题。
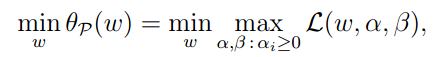
为了后边的使用，我们定义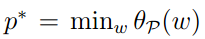
为原问题的结果。
下面，我们介绍一个和原问题稍微不同的问题，我们定义：
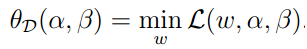
则对偶最优化问题为：
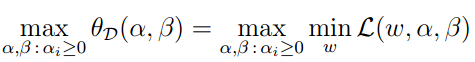
同样，我们定义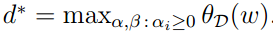
为对偶问题。原问题和对偶问题的结果有以下关系：
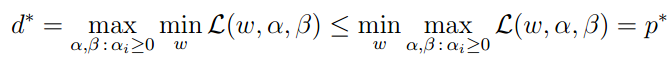
然后，在一些情况下，我们可以得到p=d，也就是说我们可以通过解决对偶问题解决原问题。
假设：
- f和gi是凸函数。
- hi是affine函数（
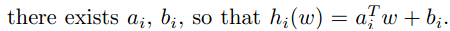）。 - 对于所有的i，存在w是gi（w）<0
在以上的假设前提下，一定存在w，α和β使w是原问题的解，α和β是对偶问题的解并且原问题和对偶问题的最优值相等：
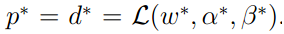
同时，w，α和β*满足KKT条件：
,
和
。这里的下标i不代表着第i个样本，而代表着第i个特征(word)。和下面的变量j对应。
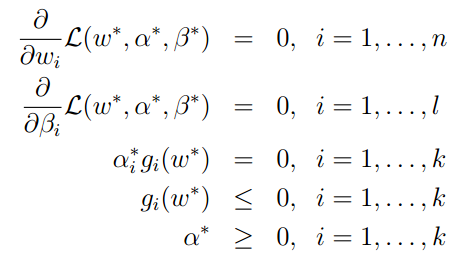
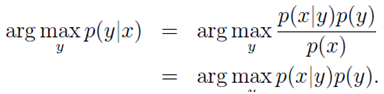
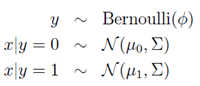
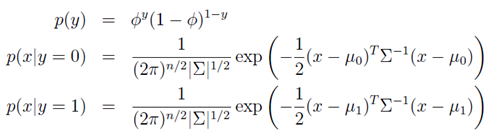
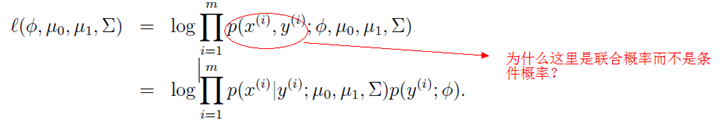
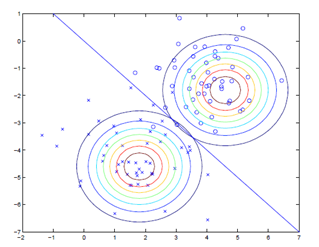
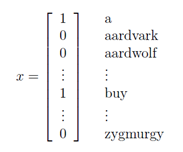
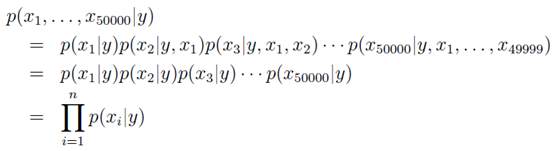
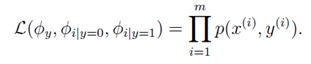
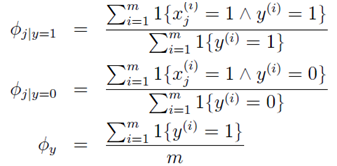
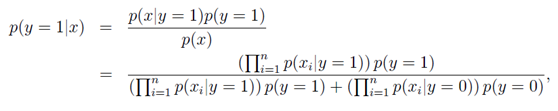
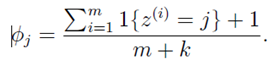
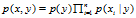
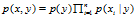。虽然此模型的邮件概率同上一个模型一样，但是变量所代表的含义不相同。
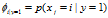for any j, 
和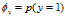
。
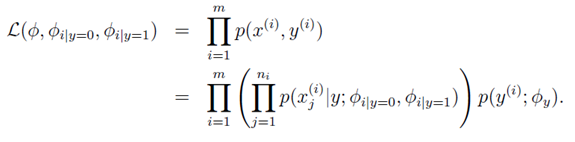
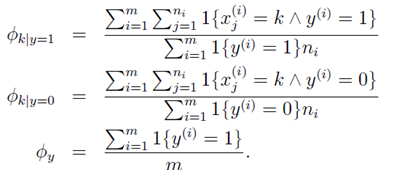
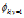的物理意义：分子是所有垃圾邮件的样本中单词Xj=k出现的次数。分母是所有垃圾邮件的单词数。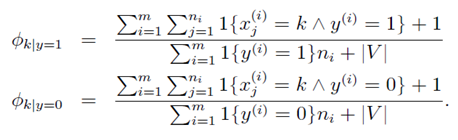
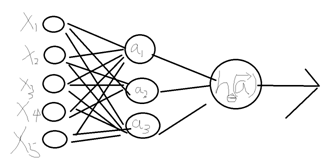
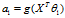
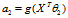
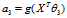
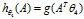
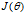最小。
（X0=1）
即可。
最接近y。提出：
的可能性的乘积。
最小即可。
，
，
这个不太像一个假设，更像一个设计。
