因子分析(factor analysis)是一种数据简化的技术。它通过研究众多变量之间的内部依赖关系,探求观测数据中的基本结构,并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。原始的变量是可观测的显在变量,而假想变量是不可观测的潜在变量,称为因子。
1 问题
在我们以前在混合高斯模型中使用EM算法时,都认为我们有足够数量的样本来找到高斯分布,比如一般认为训练样本数量m远大于样本空间维度n。但是如果n大于或等于m时,使用原来的方法就无法获得结果。比如,我们希望从数据中构建一个单高斯分布模型(比混合高斯分布要求更少的数据),通过使用以下公式获得高斯分布的参数:
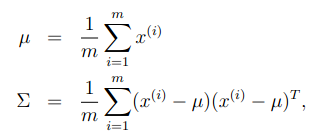
计算发现,∑是奇异矩阵,因此就无法计算高斯分布的概率分布。因此,无法使用极大似然估计的方法构建高斯模型。
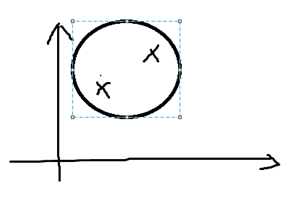
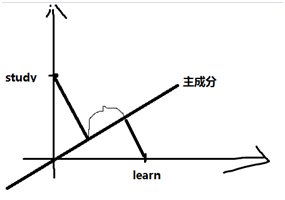
如下图,我们在二维空间上有两个样本,对其进行高斯建模后获得的模型就是一个非常长,非常窄的高斯模型,几乎就像一条直线。可以理解为高斯模型认为样本较大概率落在两点间的直线上。
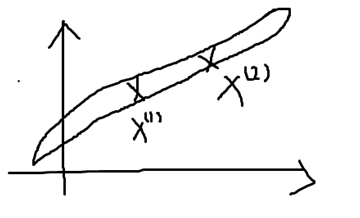
2限制∑
有上面的分析可以看出,无法构建高斯模型的原因主要是因为计算出来的∑是奇异的。那我们可以对其进行一些假设和约定,可能获得一些比较好的高斯模型。
我们可以约定∑是对角矩阵。也就是说,各特征之间互相独立,我们只需要计算各特征的方差即可,非对角线元素为0。
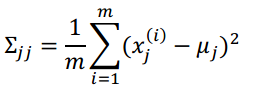
高斯分布的密度曲线是椭圆的,如果∑是对角矩阵,则这些椭圆的轴与横纵坐标平行。如下图所示
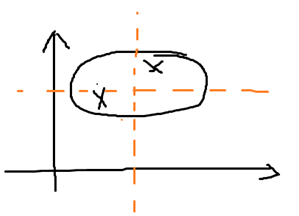
我们进一步对∑进行限制,我们不仅要求 ∑ 是对角矩阵,还要求对角线上的元素相等,即∑=σI。
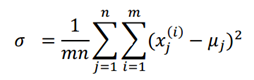
对于上面的那个例子,我们获得的密度曲线如下,密度曲线是一个圆形:
然后,对参数∑的限制同时代表着我们认为样本的不同特征向量之间是没有相关的互相独立的,但我们往往想从样本中发现不同特征向量之间的关联关系。
下面,我们将描述因子分析模型,该模型使用更多的参数来发现特征间的相关性,并且不需要计算完整的∑。
3 边缘高斯分布和条件高斯分布
在介绍因子分析模型之前,先介绍下多元高斯分布中的边缘分布和条件分布。
假设,随机变量向量x可分为两个向量:
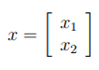
假设,x~N(u,∑),
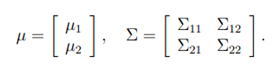
(推导过程不介绍了)结论:
多元高斯分布的边缘分布仍然是高斯分布:x1~N(u1, ∑11)
条件分布:x1|x2~N(u1|2, ∑1|2).
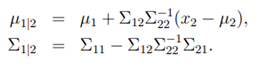
4 因子分析模型的思想和举例
下面我们通过一个例子说明因子分析的思想。
在因子分析模型中,我们认为m个n维空间特征的样本x(i)(x1(i),x2(i),….xn(i))的产生过程如下:
l 首先在一个k(k<n)维空间特征下产生m个样本:z(i),同时z(i)~N(0,I)。
l 然后通过一个变换矩阵A(n*k维矩阵),将z(i) 映射到n维空间,即A*z(i)。
l 然后在A*z(i)基础上加上均值μ(n维),即μ+A*z(i)。
l 在真实空间中,现实数据和模型相比往往具有一些误差和噪音,我们认为这些误差也是高斯分布。e~N(0,φ),u+A*z(i)+e
l 经过这些变换,才是我们的真实的样本x(i)=μ+A*z(i)+e
下面以图例解释上述步骤,假设我们有m=5个2维样本x(i),即两个特征。
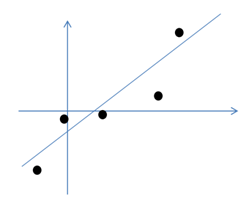
1. 首先我们认为在1维空间,存在正态分布的5个z(i)。均值为0,方差为1。

2. 然后使用某个A=(a,b)T将一维的z映射到2维,图形表示如下
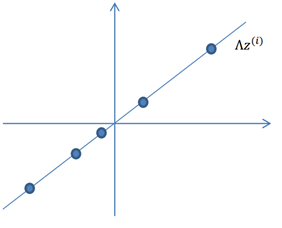
3. 加上μ(μ1,μ2)T,即将所有点的横坐标移动μ1,纵坐标移动μ2,将直线移到一个位置,使得直线过点μ,原始左边轴的原点现在为μ(红色点)。
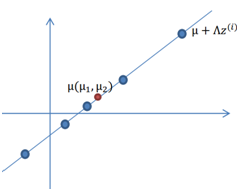
4. 然而,显示和模型相比会有一定偏差,因此我们需要将上步生成的点做一些扰动(误差),扰动e~N(0, φ)。加入扰动后,我们得到黑色样本x(i)如下:
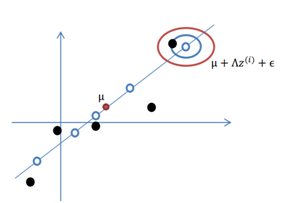
其中由于z和e的均值都为0,因此μ也是原始样本点(黑色点)的均值。由以上的直观分析,我们知道了因子分析其实就是认为高维样本点实际上是由低维样本点经过高斯分布、线性变换、误差扰动生成的,因此高维数据可以使用低维来表示。
5 因子分析模型
根据上一节的解释,我们定义因子分析模型为隐含随机变量z经过随机变换和扰动得到的样本x,其中z就是因子,维度比x更低:
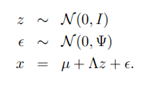
定义z和x的联合分布为联合高斯分布:
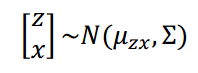
计算两个参数,(计算过程略)可知
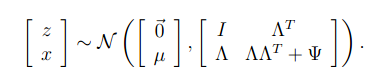
根据上式和我们对边缘高斯分布的定义和推导可知:x~N(u, AAT+ φ)。
因此,对于一个训练集,似然估计为
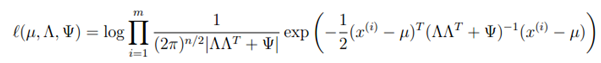
为进行最大似然估计,我们希望分别根据三个参数对上式求最大值。但是无法求上式的最大值(我反正不想试。。。)。因此使用EM算法。
6 EM算法在因子分析的使用
因子分析的原理理解了,如何去求解因子分析我认为不是最重要的,这里是使用EM进行求解。
|
初始化三个参数;
循环重复直至收敛{
(步骤E)对于每一个i(样本),计算:
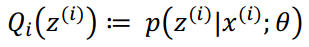
(步骤M)针对三个参数最大化:
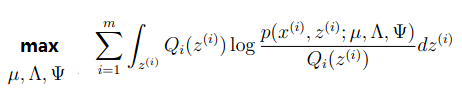
}
|
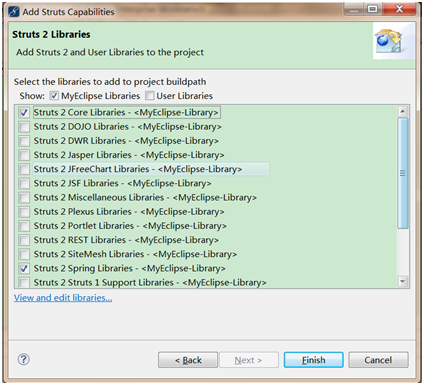
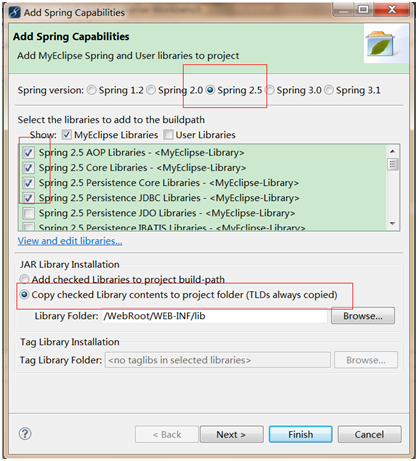
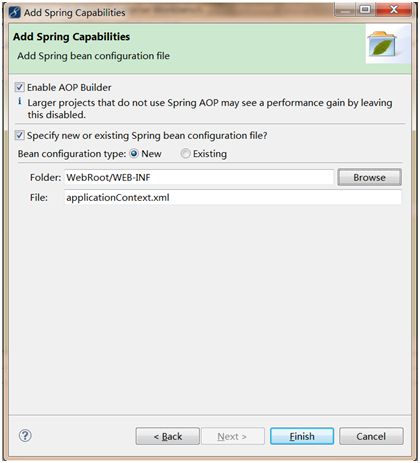
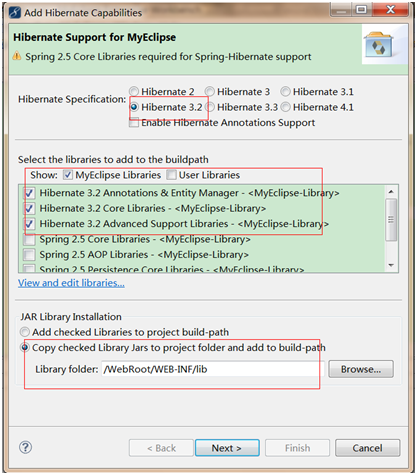
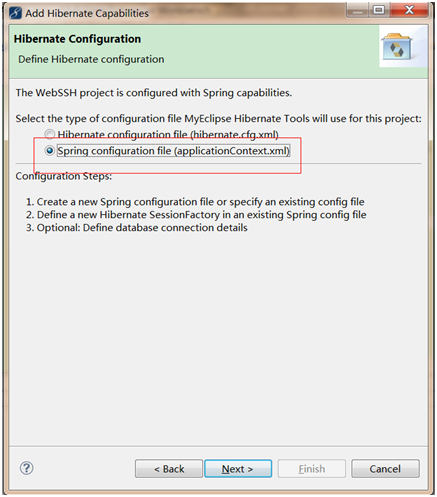
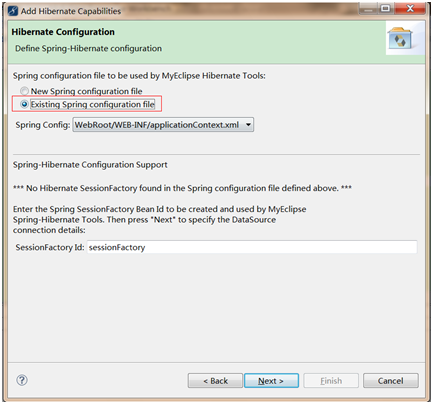
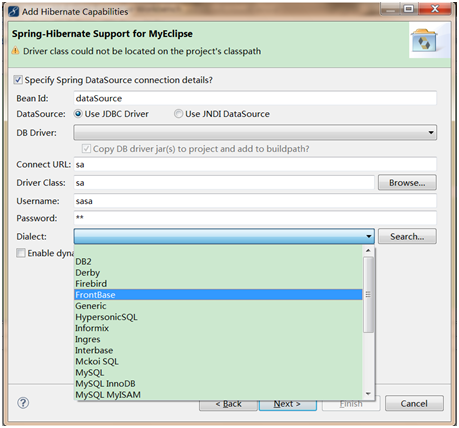
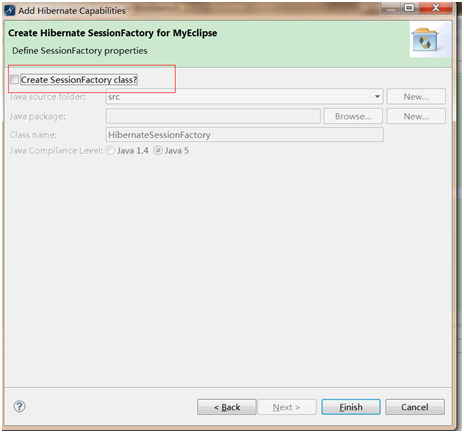

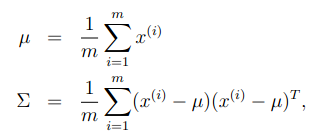

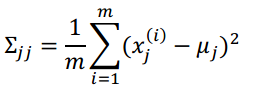

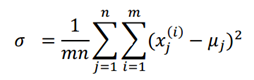

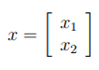
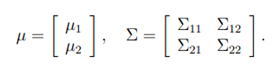
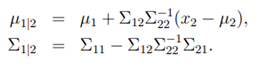





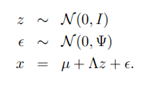
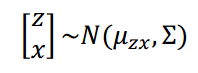
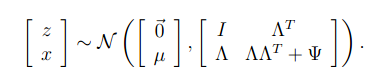
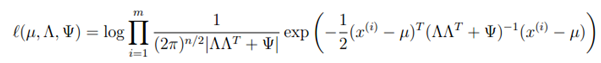
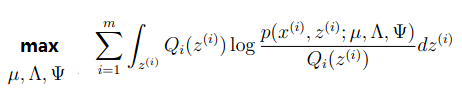


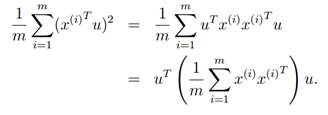
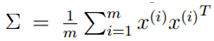 ,而u为单位向量,则上式的最大值代表着∑的非特征值,u代表着主特征向量(特征值最大的特征向量)。
,而u为单位向量,则上式的最大值代表着∑的非特征值,u代表着主特征向量(特征值最大的特征向量)。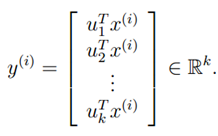
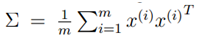

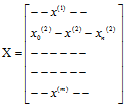




 (常数)
(常数)







 ,
, ,
, 和
和 。
。





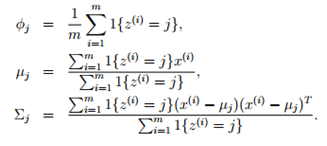

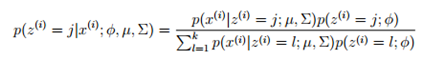





 的评价的稀疏性。
的评价的稀疏性。 ,P(u,i)表示传统的CF打分(可使用全局的,也可以基于用户划分使用),TravelPenalty(u,i)表示u和i的距离。
,P(u,i)表示传统的CF打分(可使用全局的,也可以基于用户划分使用),TravelPenalty(u,i)表示u和i的距离。