NP问题

预备知识

判断/最优问题

有些问题的答案只有两种，yes or no。对于这种问题，称为判断型问题。还有些问题目的是求出最优解，比如最短路径等，称为最优型问题。为了简化NP问题的讨论，我们将所有的问题都限定在判断型问题上。这种限定是科学的，因为所有的最优问题都可转化为判断问题。

Example：

一个优化型问题定义如下：给定一个有向图G(V, E)以及V中两顶点s和t，找出一条从s到t的简单路径使得它含有的边最多。

把上述优化问题定义为一个判断型问题

假设(a)中的判断型问题有多项式算法A，请用算法A为子程序，设计一个多项式算法来解决对应的优化问题。

(a)我们引入一个变量k后，这个判断型问题可定义如下：

给定一个正整数k和有向图G(V, E)，以及V中两顶点s和t，是否存在一条含有至少k条边的从s到t的简单路径？

这个算法分两步，第一步确定最长的路径含有的边的个数k，第二步把这条最长路径找出来。做法是，对图中每一条边进行测试。如果把这条边刪去后，图中仍有一条长为k的路径，则将它刪去，否则保留。当每条边都测试后，剩下的边必定形成一条长为k的路径。

编码和语言

在计算机解决问题时，所有的问题都需要对问题进行编码表示。因此，对于一个判断性问题p，我们可以使用x表示其编码。

反之，给定一个子符串x，可以有三种情况：(1) x代表问题p的一个实例并且有答案yes；(2) x代表问题p的一个实例并且有答案no；(3) x不代表问题p的一个实例，只是一个杂乱的子符串而已。对第(1)种情况，我们用p(x) = 1表示，而用p(x) = 0表示另两种情况。

定义：给定一个判断型问题p，它对应的语言L(p) 是所有它的实例中有yes答案的实例的子符串编码的集合，即L(p) = {x | x ? S* and p(x) = 1}。

多项式归约

给定两个语言L1和L2，如果存在一个算法f，它把S*中每一个字符串x转换为另一个字符串f(x)，并且满足

• x ?L1 当且仅当f(x) ?L2，
• f是个多项式算法，即转换在多项式时间内完成，

那么，我们说L1可多项式归约到L2，记为L1 ￡p L2，f称为多项式转换函数或算法。

如图14-2所示，转换函数f把S*中每一个字符串映射到另一个字符串。注意，这个映射不要求单射(one to one)，也不要求满射(onto)，但一定要把L1 内的一个字符串映射到L2 内的一个字符，把L1 外的一个字符串映射到L2 外的一个字符串。

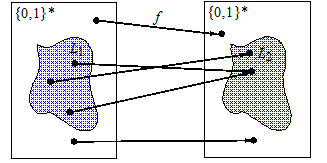
图1 多项式转换函数f必须分别把L₁ 内和L₁ 外的字符串映射到L₂ 内和L₂ 外

P问题

P语言类(class P)是所有可以被一个算法在多项式时间内判定的语言的集合，即P = {L | L í S* 可被一多项式算法所判定}。如果语言L可以被一个算法在多项式时间内判定，那么L被称为属于P类的一个语言。

如果问题p对应的语言L(p)属于P类，那么问题p也称为P类问题。

P问题代表着这个问题可以被确定性图灵机在多项式内解决。

NP问题

NP问题是可以被非确定性图灵机在多项式时间内解决的问题。

非确定图灵机是一个理论模型，与确定性图灵机不同在于转换函数，确定性图灵机的转换函数是一对一的，而非确定性图灵机转换函数是一对多的。一个问题可以使用非确定型图灵机解决，我们可以将非确定性图灵机的状态路径树看作问题的遍历。

使用非确定性图灵机证明NP问题往往非常复杂，一般使用多项式检验机模型。

多项式检验机的输入除了问题的编码以外，还要求输入一个证书。证书是用来证明问题可以得到yes的回答。只要设计出了一个检验算法可以验证这个证书的正确性，那么这个问题就是NP问题。

例：证明判断有向图G(V, E)是否有哈密尔顿回路问题属于NP类。

证明：????如果G(V, E)有哈密尔顿回路，它通过每个顶点正好一次，那么我们可以把这个回路作为证书来验证。我们用p表示有n个顶点的序列并作为输入的证书。多项式检验算法的伪码如下：

Hamilton-Cycle-Verification (G(V, E), p)

1. 检查是否有|p| = |V|
2. 检查 p 中每个顶点是否属于集合 V
3. 检查V中每个顶点是否在p中出现
4. 检查从p中每个顶点到下个顶点是否是E中一条边
5. 检查从p的最后一个顶点到p的第一个顶点是否是E中一条边
6. 如果第1步到第5步的答案都是yes，那么输出1，否则输出0
7. End

?这个模型和非确定性图灵机在本质上是相同的。因为在非确定性图灵机中，我们有很多状态路径，如果问题有一个解，那么这个问题就是NP问题。那么我们假设已经找到了这个解作为证书，那么我们就可以使用确定性图灵机来判断这个证书。

其实，我们在现实中遇到的问题几乎全部都是NP问题，非NP问题只在理论上存在，实践中除非复杂性计算方面的科研项目才可能遇到。所以，一般问题都是NP问题，证明只是为了更加严谨。

NPC问题

NPC问题是NP问题中最难的问题，所有的NP问题都可以多项式归约到NPC问题，而且NPC问题之间也可以互相归约。

目前为止，人们还不知道是否有一个NPC语言L可以被一多项式算法所判定，也不能证明任何一个NPC语言L不可能被一多项式算法所判定。因此，如图14-4所示，集合P，NP，和NPC的关系有两种，但大部分人相信第二种(图14-4(b))，但有待证明。

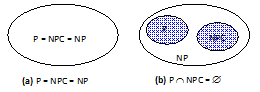
图2 集合P、NP、和NPC的两种可能的关系

NPC问题证明

根据NPC的定义，我们如果要证明一个问题是NPC，首先要证明这个问题是NP问题，然后证明所有的NP问题都可以归约到这个问题。

证明NP问题比较简单，但是证明所有的NP问题都可以归约这个问题相对比较复杂。但是，我们可以利用已知的NPC问题，因为所有的NP问题都可以归约到已知的NPC问题，如果已知的NPC问题可以归约到新的问题，那么新的问题也是NPC问题。

利用已知NPC问题证明新的问题是NPC问题的思想如下：

找到新问题对应的判定性问题，将已知的NPC通过某种变化变成新问题的某一特例，并保证已知NPC问题成立当当且仅当新问题成立。

将已知NPC问题变为新问题特例没有一个通用的方法，找到这种方法需要一些技巧，也需要一些经验甚至灵感。