3D中的矩阵变换

Published: 13 Mar 2014 Category: 游戏研发

我以前写过一篇关于D3D空间变换的文章主要讲了D3D中怎么使用三种变换，将物体本地坐标转为用户可观察的画面，但是并没有讲具体的原理。这篇文章分析一下空间变换的原理。

空间变换就是将物体本地坐标通过矩阵变换，将这些坐标转为世界坐标（世界变换），然后将世界坐标转为观察坐标（取景变换），最后将观察坐标转为屏幕的上的投影（投影变换）。

矩阵变换

所有的变换都是通过矩阵变换计算的。比如，我们可以将任何一个点(x,y,z)转为另一个点(x', y', z')，只需要使用一个4*4的变换矩阵：

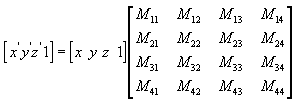
上式会使用矩阵的乘法将坐标点进行转换：

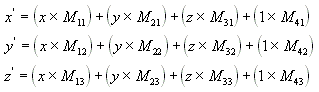
常见的变换主要有：移动、旋转和缩放，对于这三种变幻都有对应的变换矩阵以实现效果，同时也可以将矩阵进行相乘，从而获得一个综合效果的变换矩阵。

移动

下式可以将点(x,y,z)移动到(x', y', z')，移动的距离分别为(Tx,Ty,Tz):

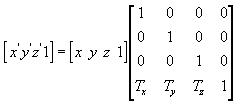
那个四维矩阵就是转移矩阵，我们可以使用D3D中的Translate函数获得这个矩阵。

D3DXMATRIX Translate(const float dx, const float dy, const float dz) {
    D3DXMATRIX ret;

    D3DXMatrixIdentity(&ret);
    ret(3, 0) = dx;
    ret(3, 1) = dy;
    ret(3, 2) = dz;
    return ret;
}    // End of Translate

缩放

可以使用下式将点(x,y,z)沿着x、y、z轴所放到(x', y', z')，一个点体现不出来缩放功能，但是若对一个三角形的三个定点都同时计算，则体现了缩放功能：

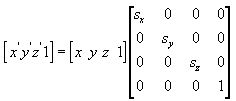
使用函数D3DXMatrixScaling获得缩放矩阵。

旋转

下面的描述针对左手坐标系统。

以下三个公式分别是将点基于x轴、y轴、z轴旋转。

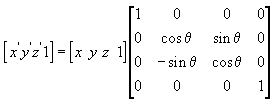
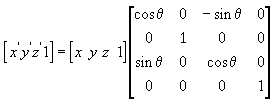
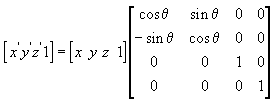
在D3D中，分别用函数D3DXMatrixRotationX, D3DXMatrixRotationY和D3DXMatrixRotationZ来创建旋转矩阵。

世界变换

物体原本是基于本地坐标创建的，转为世界坐标，只需要把物体的所有的顶点世界变换矩阵就是根据需要对这个物体的操作（移动、旋转或缩放），创建相应的变换矩阵，然后物体的原坐标与这些变换矩阵一次相乘，则变换为我们想要的坐标。

摄像机、观察矩阵与取景变换

摄像机就是我们的眼睛，取景变换就是把世界坐标系里面的点转换到以我们的眼睛为参照物的坐标系的世界里面。

比如，一个顶点的x坐标为10，假设摄像机的位置为5，并且摄像机的方向为x正方向，那么这个定点在摄像机的世界里，x坐标为5。

综上所述，取景变换分为两步：

在世界坐标系中的所有对象，都以摄像机为参照点移动，使摄像机为坐标原点。
使所有的对象随着相机旋转，使照相机的观察方向为z轴正方向，并且相机的UP向量指向Y轴正方向。

经过以上两步，对象的世界坐标就变成了观察坐标系中的坐标了。

一般来说，我们都是使用函数D3DXMatrixLookAtLH来创建一个观察矩阵，该函数其实就是创建可以实现以上两步的变换矩阵。

D3DXMatrixLookAtLH(MOut As D3DMATRIX, VEye As D3DVECTOR, VAt As D3DVECTOR, VUp As D3DVECTOR) 
zaxis = normal(At - Eye)
xaxis = normal(cross(Up, zaxis))
yaxis = cross(zaxis, xaxis)
MOut=
 xaxis.x           yaxis.x           zaxis.x          0
 xaxis.y           yaxis.y           zaxis.y          0
 xaxis.z           yaxis.z           zaxis.z          0
-dot(xaxis, eye)  -dot(yaxis, eye)  -dot(zaxis, eye)  1

参考： http://blog.csdn.net/razor87/article/details/16853167

透视投影变换

透视投影变换是将观察空间中的物体映射到投影面上，相当于使用一个照相机对着观察空间照相获得一个照片。

投影变换由两步构成：

用投影变换矩阵把顶点从视锥体中变换到裁剪空间(Canonical View Volume，CVV)中，如下图所示。CVV：一个正方体，openGL中x/y/z的范围都为[-1,1]。
CVV裁剪后进行透视除法。

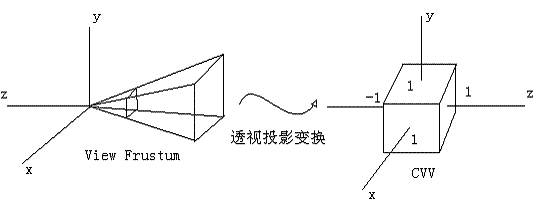
下图表示了视锥体中的顶点p映射到界面np中的点p'。

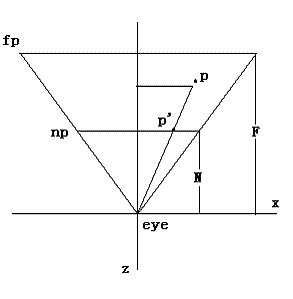
上图是右手坐标系中顶点在观察空间中的情况。其中eye——研究位置，np——近裁剪截面，代表着相片，fp——远裁剪截面，N为近裁剪截面与眼睛的垂直距离，F为远裁剪截面与眼睛的垂直距离。其中，p'坐标Z=N。

存在关系：

x/x' = z/z' = z/-N

则，x'=-N*x/z

同理，y'=-N*y/z

因此，p'=(-Nx/z,-Ny/z,-N)

p'的z坐标恒为-N，因此没有必要存储。

但是，虽然p点投影到了p'后，z坐标恒为-N，但是p的z坐标在以后的处理中是有用的，因为不同的顶点p1、p2投影到np上可能都为p'，但是p1和p2具有不同的z值，从而产生遮盖。因此，z只需要保存。

所以，我们使用p'的z值存储p的z值，令p'=(-Nx/z,-Ny/z,z)